In the last blog post, we began laying out the groundwork for what will become an argument that Schnorr signatures are secure. We discovered the Schnorr Identity Protocol and proved that it is secure and correct (specifically Complete, Sound, and Honest-Verifier Zero-knowledge). It is very unlikely that this blog post will make much sense if you have not yet read the previous post, so go read it if you haven’t already.
In this post, we will complete our argument by converting our ID scheme into a signature scheme and arguing that our conversion from a correct ID protocol will result in a correct signature protocol.
With this argument complete, we will then use the remainder of this Schnorr blog series to explore various tweaks to Schnorr signatures that allow all sorts of cool protocols and use-cases in Bitcoin!
Schnorr Signature Series:
What are Schnorr Signatures – Introduction
Schnorr Signature Security: Part 1 – Schnorr ID Protocol
Schnorr Multi-Signatures – MuSig
Scriptless Scripts – Adaptor Signatures
Flexible Round-Optimized Schnorr Threshold – FROST
Taproot Upgrade – Activating Schnorr
From Schnorr Identification to Schnorr Signatures
The previous post should have convinced us that the Schnorr Identification Protocol is a valid and secure identification protocol as it is Complete, Sound (under DLOG assumption), and HVZK. So we now live in a pretend world where not only did we discover that the DLOG problem is hard for Elliptic Curves but we have a way of using this fact to identify people using their public keys. But now we want to go a step further and create a digital signature scheme. Our identification protocol seems like it is very close to being a signature protocol so we decide to try and convert it into a signature scheme by using a couple modifications.
There are two main differences which must be modified between identification protocols and signature protocols:
- Signatures protocols are non-interactive whereas identification protocols are a back-and-forth conversation.
- Identification protocols only prove knowledge of a private key while signatures protocols also commit to a message.
To address the first difference, there is a common modification of protocols like Schnorr ID which converts interactive protocols into non-interactive ones by replacing the challenger with a hash function. Specifically, if there is an interactive protocol where the verifier/challenger’s only role beyond accepting or rejecting at the end is to provide random challenges, we can replace their challenges with outputs of hash functions which we assume to be ideal functions. But what are the inputs to these hash functions? We use the existing context as the input to the hash function, meaning we take all things that have been said so far and hash them to generate our challenges without needing a challenger. This modification is called the Fiat-Shamir Transform. We now have a non-interactive identity protocol where
- Prover generates a random number k, and puts R = k*G in the context
- Prover hashes the context, computing H(R), and uses it as the random challenge, e
- Prover computes a number s using their private key, k and e and publishes (R, s) as their identity proof
- Any verifier checks if s*G =? R + H(R)*X accepting if this is true and rejecting otherwise
Now all we need to do is modify this non-interactive protocol to also commit to a message. We do this by simply adding the message being signed, m, to the context! The result is a signature scheme where the prover generates a random k, computes H(R, m) as their challenge, computes s = k + H(R, m)*x and publishes (R, s) as their signature. A verifier can then verify this signature by checking whether s*G = R + H(R, m)*X which may look familiar to you as this is the Schnorr signature scheme!
One final note I want to make is that oftentimes (as is the case with BIP 340) the public key X of the signer is also included in the hash as part of the context. For an explanation of why this is important for Bitcoin, see the “Key prefixing” section of BIP 340.
Security of Schnorr Signatures
So that’s neat, we have another way of thinking about Schnorr signatures as a modification of an identification protocol, but does this help us in proving their security? Why yes it does, we now not only have another way of thinking about Schnorr signatures intuitively but we have an explicit relationship to a protocol that we already proved to be secure! So now all we have to do is argue that the relationship between Schnorr signatures and the (secure) Schnorr ID protocol implies that Schnorr signatures must also be secure.
But first, what does it even mean for a signature scheme to be secure? A natural first property would once again be Completeness, i.e. that if a signer truly knows a private key x then their signature should cause any verifier to accept their signature. Well the Fiat-Shamir transform from our ID protocol to our signature protocol does not affect this property as a prover/signer who could correctly participate in the ID protocol will be able to generate a valid signature.
The second property we might want is once again Soundness, i.e. that an impersonator who does not know x cannot generate a valid signature. In the context of digital signatures Soundness is usually referred to as Unforgeability. Once again this property is unaffected by the Fiat-Shamir transform as our argument reducing Soundness of the ID protocol to the DLOG problem carries through for signatures as well (under valid hash function assumptions).
But we actually want a stronger property than run-of-the-mill Unforgeability, we want an impostor to be unable to generate a forgery even if the impostor has access to an arbitrary number of previous signatures by our key for messages of the impostor’s choice. This property is often referred to as EUF-CMA which is short for Existential UnForgeability under a Chosen Message Attack.
We will prove Schnorr signatures are EUF-CMA secure by reduction to an attack against the Schnorr ID protocol which we already know how to convert into an attack against the DLOG problem. This time our black-box is an EUF-CMA forger which makes a bunch of requests for signatures which it takes as inputs, then it outputs a valid forgery with some probability p. We wish to use this black-box to do an impersonation attack against the Schnorr ID protocol (which we already know to be reducible to an attack on the DLOG problem).
We will model our hash function as a random oracle (see Random Oracle Model) which is a black-box that takes an input and spits out an output. Given the same input twice we require the random oracle to give the same output, and given any input we require the output to be truly random. In other words this black box is a function from inputs to outputs where there is no relationship between inputs and outputs (there is just a random arrow going from each input to some random-looking output).
This may be a reasonable heuristic for how a hash function should work as it contains all the elements that we expect out of a cryptographically secure hash function. However, when we prove things in the Random Oracle Model, things can get pretty unintuitive. All hash computations are replaced with queries to a random oracle and the value returned does not actually have to be truly random so long as it is random to the entity making the random oracle query. For example, if there are two parties Alice and Bob in some protocol and Bob generates a random value, r, we can use this value r in response to a random oracle query from Alice. This is unintuitive because it isn’t how hash functions work at all, but when we are proving things in the Random Oracle Model we aren’t dealing with real hash functions, we are dealing with these weird oracle entities which can do such things. In other words, a security result in the Random Oracle Model is more of a heuristic for security rather than a true Mathematical proof.
Thus our list of “given”s that we need to prove our security are that hash functions can be modeled accurately as random oracles and that the DLOG problem is hard, but these are the only assumptions we need to prove Schnorr is secure! (More are required for schemes like ECDSA). Both of these “given”s are already internally used by Bitcoin (and many other things) so these are generally viewed as acceptable assumptions. This is the model in which we shall prove Schnorr signatures secure.
Finally the moment we’ve all been waiting for, time to prove that Schnorr is secure! Let’s go over this at a high level first, and then fill in some details after. First, let us examine the black box which can forge Schnorr signatures with some non-negligible probability. Before it produces a forgery, the black-box is allowed to make queries asking for signatures of various messages of its choice (this is because we assume our attacker is allowed to have access to such information). After the signature queries, it then begins to compute a forgery and during this computation it is also allowed to make some number of queries to a random oracle (as that is how we are modeling hashes). Once all of the signing and random oracle queries are completed, it then produces a signature forgery that will be valid some non-negligible percentage of the time. This is the black box we are given, and we wish to use it to construct a machine which can impersonate the public key X in the Schnorr ID protocol.
We will do this in two steps: First, we will initialize our black box for forgery by simulating signatures for each of its starting queries and answering all of its random oracle queries with random values. Second, one of the black box’s random oracle queries will be to compute H(R, m) and we will take this R and send it to our Schnorr ID challenger, who will respond with a random value e. We will return this random value e as the result of the random oracle query for R || m and in the end, we will get a valid forgery s which passes the check s*G = R + e*X which happens to be the verification that it must pass for both Schnorr signatures and the Schnorr ID protocol in the case where e = H(R, m)!
This argument skipped some key details, however. How do we simulate signatures to satisfy the black box’s first stage? How can we be sure that all random oracle query responses in the second stage follow the Random Oracle Model rules? How do we know which random oracle query will contain our message and R value? To answer these questions, let’s go through this argument with more details.
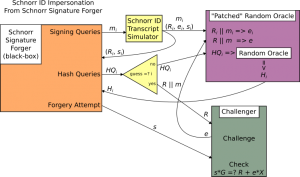
Our black-box (Schnorr forgery) attacker demands some number of signatures for some specific messages, let’s call the ith message mi. We (the people trying to do a Schnorr ID impersonation using the black-box) respond by forging a bunch of random Schnorr ID transcripts, let us call the ith simulated transcript (Ri, ei, si) where this transcript is computed in the way described in the last post. We will use these simulated transcripts, along with our power to answer random oracle queries, to simulate signatures. Specifically we keep in memory that any random oracle query in the future for the value Ri || mi maps to ei and we return (Ri, si) as our response to the black-box’s signature query.
Once this is done the black-box moves on to its random oracle queries (after which it will produce a signature forgery (attempt).
We keep track of every query and its response to ensure that if it ever asks for the same hash twice we return the same thing and if it ever asks for Ri || mi (from the first stage) we return ei . Now we begin our attack on the Schnorr ID challenger which requires an R value from us to start.
One of the black-box’s random oracle queries will be the hash of R || m (where those are the values for which the forgery is being produced). We make a random guess ahead of time for which query will be the one containing R and m in this way and we will be right with some non-negligible probability (If the black-box makes Q random oracle queries we have a 1/Q chance of guessing correctly). Rather than returning an actual random value for this query, we first send this guessed R value to the Schnorr ID challenger. It responds with a random value e which we return to the black-box in response to its random oracle query for the hash of R || m which is an acceptable response because the value e is random so that the black-box will not be able to tell the difference between this and interacting with a true random oracle. Now when the black-box produces a forged value for s, it has probability p to be a correct forgery and this gives the value s a probability of p*(some non-negligible number) of being a valid response to the Schnorr ID challenger! This non-negligible number is less than 1 is due to our choice of black-box oracle query (as well as a couple details I skipped).
To recap at a high level, given a Schnorr forgery black-box, we can initialize it using simulated Schnorr ID transcripts, then we can look at its forgery computation (specifically its calls for hashes) and make a decent guess as to what R value it will be using in its forged signature and what message, m, it is forging a signature for, and lastly, we can use this guess to initiate a Schnorr ID protocol with a challenger who will respond with a random challenge, which we will tell our black-box is the hash of (R || m) so that if it produces a valid signature forgery, we will be able to use the signature s value as a valid response to the Schnorr ID challenger and successfully execute an impersonation! Thus, if a black-box exists which has a non-negligible probability of forging Schnorr signatures, we can use the program described as a reduction above to construct a black box which can attack the Schnorr ID protocol. And in turn, this black box will allow us to attack the DLOG problem with non-negligible probability as described in the previous blog post (by forging two signatures for the same R value, succeeding some significant portion of the time, which will leak the private key). Therefore, in the Random Oracle Model, if the DLOG problem is hard, then Schnorr signatures are EUF-CMA secure and secure enough for Bitcoin!
I hope that this rather lengthy argument serves to convince the reader that Schnorr signatures are secure, and gives you an idea of what that means with quite a bit of precision. I encourage the reader to ask questions if you have them, there are many places these questions can be asked: you could join our slack and ask in the cryptography channel, you could ask a math-savvy friend, ask on an IRC channel, tweet a question, email me or someone else who knows, etc. If you are looking for further reading materials that go even deeper skipping fewer to no details of the Schnorr security proof, I personally recommend the two resources I most heavily used in preparing this blog:
- Waxwing’s blog post on this topic
- Boneh-Shoup chapters 18 and 19
One of my goals in writing this blog post was to prepare people who would have trouble reading technical content such as the above (if they are interested). Another goal was to serve up a Schnorr security proof in the most accessible terms I could muster to reach a larger crowd than the above resources, though I will admit that there is no way to get around many of the complexities of such a precise argument.
Now that we have quite fully fleshed out “vanilla” Schnorr, the rest of this blog series will take 10 steps back out of the weeds and look (much) more casually at the countless variants on the Schnorr signature protocol that enable all of the cool things there are to be excited about with Schnorr’s integration into Bitcoin!

