In the previous post of our introductory Schnorr series, we discussed the definition of Schnorr signatures and tried to build some intuition as to how Schnorr signatures work by looking at a sequence of choices that could have led us to the definition. In this post we will go even deeper and begin an argument for Schnorr’s security by deriving the signature scheme from yet another angle.
Schnorr Signature Series:
What are Schnorr Signatures – Introduction
Schnorr Signature Security: Part 2 – From IDs to Signatures
Schnorr Multi-Signatures – MuSig
Scriptless Scripts – Adaptor Signatures
Flexible Round-Optimized Schnorr Threshold – FROST
Taproot Upgrade – Activating Schnorr
The argument given in this blog post and the next is not a complete or completely rigorous argument. Instead, my goal is to give most of the ideas contained in the full security proof to provide slightly less technical readers with a better intuition for why Schnorr signatures are secure with the dual purpose of preparing the interested and persistent readers to read more rigorous and technical proofs of Schnorr’s security. That said, I hope that the following argument for Schnorr’s security is still convincing to the reader that trusts me when I say that the low-level details I skip will work themselves out. After reading this post and its sequel (and presumably its prequel) you should have a pretty deep understanding of what Schnorr signatures are, how they work and why they are secure.
With this understanding in mind, the remainder of this blog series after the security argument will look at various tweaks of the Schnorr signature scheme that enable countless use cases for Bitcoin and beyond. I will note that understanding the security of Schnorr is not a prerequisite for exploring these later things.
Before you read on, I recommend you are first comfortable with the previous blog post’s contents as I will be relying heavily on results and properties that were discovered in that post. I also recommend that you should be comfortable with the prerequisite topics linked in the previous blog post (modular arithmetic, hash functions, public keys and elliptic curves).
The last note I’d like to make before we get started is that I more-than-expect that the reader may need to reread portions of this post before feeling any comfort with this argument: this is normal when it comes to precise arguments, in preparing for writing this post I read and reread various security proofs countless times!
The Schnorr Identification Protocol
Like in the last post, let us once again pretend we live in a world in which we have just discovered the Discrete Log Problem is hard on Elliptic Curves i.e. that it is hard to reverse the process x*G where x is a big number and G is a point on an Elliptic Curve, so that we can use x*G = X as a public key for the private key x. Rather than trying to construct a digital signature scheme directly this time, let us instead take an ever-so-slightly smaller and more natural first step: to use public keys as a form of identity. After all, if it is really true that one cannot recover a private key from a public key, then there should be some way to use a private key as a kind of password which only one person knows so that they can use it as identification.
As we did last time, let us first consider what properties an identification protocol should follow. Intuitively we want an identification protocol to be a conversation between a party trying to prove their identity (i.e. that they own a private key) to a challenger similar to how websites require passwords to prove your identity. A key difference here is that we don’t want the challenger to learn your private key as they could then steal your identity, and your bitcoin! We trust websites with our passwords quite often, but we don’t want to trust anyone with our private keys!
Put more formally, an identification protocol is a conversation between a verifier (aka challenger) and a prover (who is trying to prove their identity) where
- If the prover really does know the private key they are trying to prove they know, then the verifier should become convinced – a protocol satisfying this property is called Complete
- If the prover does not actually know the private key they are trying to prove they know (i.e. the prover is an impersonator), then the verifier should be able to detect their fraudulence – a protocol satisfying this property is called Sound
- If the verifier follows the protocol faithfully and is successfully convinced, then they should learn nothing about the private key which the prover is proving they know – a protocol satisfying this property is called Honest Verifier Zero Knowledge or HVZK (this is a weaker version of true Zero Knowledge as it is meant when people talk about Zero Knowledge Proofs/ZKPs)
We might reason that for this conversation to be both convincing to the verifier, and Zero Knowledge to the (honest) verifier, each party is going to need to generate a random number. The prover’s random number will be used to mask/hide their private key from the verifier. Meanwhile the verifier’s random number will act as a challenge of some kind as we don’t want the prover to control the entire conversation, in other words the challenger’s challenge should throw a wrench in an impersonator’s attempted identification proof. Let’s call the prover’s random number k and the verifier’s random number e.
Just like we reasoned in the last blog post, we want to combine the prover’s private key, x, with the verifier’s challenge, and then we want to hide this value (because it would leak the private key) with the prover’s random value. We might do some trial and error and eventually come across the following combination: s = k + e*x which combines the challenge, e, with the prover’s private key, x, and then hides this value by adding the random value, k.
Also, like we came up with in the last blog post, the verifier should, given R and s, check that
s*G =? R + e*X
The value s should be the punchline of the conversation between the verifier and the prover but before the prover says this number, both parties must first exchange their random values. Who should go first? Well it seems reasonable that the challenger should go last as otherwise the prover might be able to use knowledge of the challenge to construct some kind of tricky non-random value that “gets around” the challenge. Thus, the identification protocol we’ve come up with is:
- Prover generates a random number k, and sends R = k*G to the verifier
- Verifier generates a random number e and sends it to the prover
- Prover computes a number s using their private key, k and e and sends it to the verifier
- Verifier checks if s*G =? R + e*X accepting if this is true and rejecting otherwise
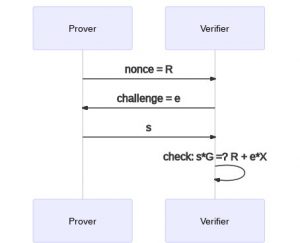
We may have some intuition that this conversation, known as the Schnorr Identification Protocol, gives a valid way of proving (in zero knowledge) ownership of a private key, but in order to gain a deeper understanding, let us consider each of our three properties in turn.
Security and Correctness of the Schnorr Identification Protocol
Completeness
The easiest property to verify for our ID protocol is Completeness. If the prover is honest (really knows the private key), then by generating a random k and receiving a random e they will always be able to compute a value for s that the verifier will accept. Namely s = k + e*x will always pass the verifier’s check. In other words by the way we constructed this protocol it is clear that an honest prover will successfully convince the verifier of their identity.
Soundness
But what about a dishonest prover/impersonator? Is our ID protocol Sound? To prove that it is sound and hence safe against impersonators, we are going to have to use the “hardness” of the Discrete Log (aka DLOG) Problem to argue that impersonation is also “hard”. Recall that the DLOG problem is the problem of computing a private key from a public key, i.e. given a point X = x*G on an elliptic curve, compute x. We will argue that this connection exists in the way cryptographers almost always do, by reduction. A problem A is reducible to a problem B if an algorithm that solves B can be converted into a program that solves A, which proves that A cannot be harder to solve than B. If we are able to do this, then that means that if A is secure, then B is secure because if B is vulnerable then A must be vulnerable by our reduction. Specifically, we wish to construct a reduction from the DLOG problem to the Schnorr ID Protocol by converting impersonation (an attack against the Schnorr ID protocol) into an attack against the DLOG problem.
Say that there is some black-box program which can be given a public key X and successfully impersonate it in a Schnorr ID conversation with some probability p. This means that the black box spits out some value R, takes in some challenge value e and then spits out a value s which will be accepted with probability p.
We wish to use this black-box to attack the DLOG problem, that is, we wish to use the black-box to compute the private key x with some non-negligible probability (if it works a non-negligible percent of the time we consider the protocol insecure). If we can do so successfully then this will mean that Schnorr ID being vulnerable implies that our public keys are as well, but we know that they are not (or at least believe this very strongly) and so we can be similarly safe believing that Schnorr ID is safe against impersonation.
So how do we use our black-box to compute the private key x? Recall the section entitled “Nonce Reuse is Forbidden” from the previous blog post. We discovered that given two correct s values, one can compute the private key x! So consider our black-box which is attempting to impersonate owning the public key X and has just given out a value for R in the Schnorr ID conversation. We know that given any challenge, e, it will successfully produce s with probability p. So let us consider two distinct challenges we could give the black-box, e1 and e2, the probability that our black-box will be able to compute correct s values for each of these challenges separately is p and so intuitively the black-box should be able to successfully impersonate both of these challenges with probability about p2 (I am skipping some details and statistical arguments but this turns out to be basically true). But wait a minute, if this black-box can successfully impersonate for X using the same nonce R for two different challenges, we know that it must be able to compute the private key x from these two s values! In other words if such a black-box existed that could break the Schnorr ID protocol with non-negligible probability, then we can convert this box into a program that breaks the Schnorr ID protocol twice with non-negligible probability and this program could then compute the private key to the public key it is impersonating. Thus we have a reduction from any impersonation attack against the Schnorr ID protocol to an attack against the DLOG problem!
Honest Verifier Zero Knowledge
We should now be convinced that our protocol is Complete and Sound (under the DLOG assumption), which leaves only to show that it is HVZK. Recall that we said this means that an honest verifier “should learn nothing about the private key which the prover is proving they know.” But that is a pretty imprecise description, how would one prove such a thing with any certainty? We must first come up with a more formal definition which captures this idea.
In cryptography, we often capture such ideas about lack of knowledge using the notion of a Simulator. Essentially we say that a party has “learned nothing at all” from a conversation if they could have simulated the other side of the conversation by themselves. To make this more concrete let’s consider the situation at hand with the Schnorr Identification Protocol. A conversation in this context is the three values (R, e, s) and we would consider this protocol to be HVZK if the verifier (who knows only X and not x) is able to generate/simulate these conversations in a way that is indistinguishable from real conversations.
Recall the end of the section “How do Schnorr Signatures Intuitively Work?” where we discovered that if the message (in this case e) being committed to was independent of everything else, then “we can generate any s value and compute an R value (using only public information) that will” result in a valid (R, s) pair. Specifically a verifier trying to simulate a prover (by generating conversations) could choose a random values s and e and then compute
R = s*G – e*X
and the triple (R, e, s) would be a valid conversation. Note that this does not mean anyone can use this simulation to impersonate a public key because the transcript that we have generated here was computed by determining the three elements out of order. This allows us to create real-looking transcripts but does not help an impersonator because in actual protocol execution, R must be the first thing computed, not the last.
But we don’t want to be able to simulate just any conversation, we want to simulate them in such a way that our simulation is “indistinguishable” from really having a conversation with a prover. To see that this way of generating conversation transcripts is really indistinguishable from real conversations, consider any valid conversation (R, e, s) and consider the probability that each method generates this transcript (one method being really talking to a prover and the other being simulation).
If we talk to a real prover (and we are an honest verifier), their choice of R will be random as will our choice of e (because we are honestly following the protocol), and then s will be a fixed value. So the probability we get this transcript is equal to the probability we make two random choices that happen to be correct. If we instead simulate by randomly choosing e and s and then computing a valid R, we end up with the same exact probability of getting our transcript because it will be the probability that we make two random choices that happen to be correct. And thus we now know that an honest verifier can simulate a prover/generate transcripts indistinguishable from real ones. This means that our interactions with real provers don’t reveal any new information to the honest verifier because anything a verifier can learn by looking at conversation transcripts they could have learned by computing fake transcripts without a prover even existing!
In this post we discovered the Schnorr Identification Protocol and proved that it is Complete, Sound, and Honest-Verifier-Zero-Knowledge. In the next post, we will convert this identification protocol into a signature protocol and use the security properties we proved here to prove that Schnorr signatures are secure!

