A couple weeks ago, we announced that we had successfully executed a DLC on-chain using oracles Bitfinex, Pierre Rochard and Suredbits. In this post, we will be diving into the details of how multi-oracle DLCs are accomplished.
Before we dive into a discussion about multi-oracle support in Discreet Log Contracts (DLCs), if you are not yet familiar with the idea and construction of DLCs we recommend you take a look at our previous blog post series or the work-in-progress DLC Specification.
As discussed in our blog about an executed volatility DLC, there is a compression algorithm which allows us to use only a handful of Contract Execution Transactions (CETs) to cover our entire payout curve. And on top of that, as was discussed in our blog post about our last DLCFD, we can optimize further using some minimal rounding.
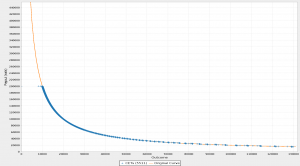
DLCs function by creating payout transactions and adaptor signatures for all possible outcomes, but when the possible set of outcomes is very large (such as the case when 3 oracles could attest to 200k possible outcomes leading to ~10 Quadrillion possibilities) compression is absolutely essential. In this context, compression refers to the grouping of many adjacent outcomes into a single outcome using digit prefixes. For example, if an outcome has 5 binary digits, then the digit prefix 010_ _ refers to all of the outcomes between 8 (01000) and 11 (01011) inclusive. This kind of compression can be applied to any consecutive interval of possible outcomes which have the same payout.
The following is a visualization of the results of such compression where the orange curve represents the original payout structure where one adaptor signature is needed for every possible outcome, and where the blue + marks represent single adaptor signatures after rounding and compression:
To better understand how we enable bounded differences between oracles, let’s explore how a DLC like this one is set up. Ben and I first agreed on contract terms such as collateral, payout curve, refund timeout, which oracles to use, and how much disagreement is allowed between oracles. We then proceeded to reduce our payout curve which mapped all possible outcomes between $0 and $262,143 (i.e. all 18-bit outcomes) to satoshi payouts. To do this Ben and I agreed on some amount of rounding (to the nearest 100 satoshis everywhere and to the nearest 1000 satoshis for outcomes above $75,000) and partitioned the set of all possible outcomes into intervals which have equal payouts (shown in red) and then ran the compression algorithm on those intervals which results in a set of digit prefixes (as compression occurs by ignoring later digits) and their payouts.

So far nothing has been different from how a regular numeric outcome DLC would be constructed for a single oracle. That is to say that these digit prefixes and their payouts represent the full set of possible outcomes in compressed form which is ordinarily used directly to construct a set of adaptor signatures on Contract Execution Transactions. To extend this set of outcomes to support multiple oracles, we use these “primary” digit prefixes and construct a set of “secondary” digit prefixes which constitute agreement.
Specifically, Ben and I have two parameters, minSupport and maxError, which in last week’s DLC we set to be 128 and 512 respectively. The minSupport parameter ensures that if any two of our three oracles were within $128 in price (as was the case), then that should constitute agreement leading to DLC execution. The maxError parameter ensures that if two oracles disagree by $512 or more in price, then this will not constitute an agreement and DLC execution cannot be completed using those two oracles. If two oracles disagree by more than $128 but less than $512 then our DLC may or may not be executed (more on this later).
Along with these two parameters, Ben and I also agreed on a preference ranking for our three oracles (1: Pierre Rochard, 2: Bitfinex, 3: Suredbits) which was made in this case using a series of coin flips, but users should chose their more trustworthy oracles to be higher in rank in general. Now if Pierre Rochard attests to a price and one of Bitfinex or Suredbits is within the allowed minSupport ($128), then Pierre Rochard’s price is used to execute the DLC. This is to say that in any set of agreeing oracles which make up a quorum, only the most preferred oracle’s outcome is used to determine payouts. If, however, Pierre Rochard does not agree with either of the others but Bitfinex and Suredbits are within minSupport ($128) then the Bitfinex price will be used to execute the DLC. In the worst case where no two of three oracles agree, then Ben and I would be forced to execute the refund branch of our DLC.
For each possible quorum of oracles, (Pierre Rochard, Bitfinex), (Pierre Rochard, Suredbits), and (Bitfinex, Suredbits), we use the digit prefixes computed via compression above to represent outcomes of the primary/preferred oracle and construct a set of digit prefixes for the secondary oracle which constitute agreement under our parameters. This is done by taking each primary digit prefix’s interval (i.e. the set of outcomes covered by that digit prefix), [start, end], and constructing a set of digit prefixes whose intervals cover at least all outcomes in [start – minSupport, end + minSupport] and at most all outcomes in (end – maxError, start + maxError) as visualized in the following diagram:
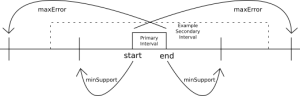
It turns out that in order to cover such a range, no more than two digit prefixes are ever required so that either there is a single secondary digit prefix which constitutes agreement with the primary oracle or else there are two of which both represent agreement. Furthermore the larger the difference between minSupport and maxError is, the greater the chances that only a single secondary digit prefix is required.
Therefore, an upper bound on the total number of DLC outcomes which require adaptor signatures will be equal to the number of (compressed) outcomes that would be required in the single oracle case, times 3 (for each possible quorum of oracles) times some number less than or equal to 2 (for the number of agreement cases which requires either 1 or 2 adaptor signatures). In all, my DLC with Ben required 14,826 adaptor signatures each of Contract Execution Transactions, totalling about 5 MB each.
This algorithm for constructing agreement outcomes for secondary oracles from a given primary oracle outcome may seem odd because it provides perfect guarantees for differences between oracles of less than minSupport or greater than maxError but for all differences in-between, no strict guarantees are made. It may appear that it would have been nicer to have more strict bounds (such as something closer to minSupport equal to maxError) but it turns out that there is a fundamental tradeoff between the number of outcomes requiring adaptor signatures needed and the tightness of the agreement bounds.
The algorithm I developed for constructing agreement requires no more than 2 adaptor signatures for any given primary oracle outcome, but in return it requires that maxError must be at least twice as large as minSupport (where generally the bigger maxError divided by minSupport is, the fewer adaptor signatures are needed). There is a variant of my algorithm which allows for arbitrarily tight bounds but it often requires many secondary digit prefixes (and consequently adaptor signatures) for every primary oracle outcome, sometimes so many as 20 adaptor signatures in place of 1 or 2 which could easily have made our 5 MB files into ~100 MB files (and would have taken an even longer time to compute and verify). Furthermore such an algorithm scales exponentially worse to more than two oracles, and so we’ve decided to optimize for the number of required adaptor signatures for now and require looser oracle agreement bounds.
One last property of this multi-oracle scheme is worth mentioning: everything happened privately client-side! The three oracles that were used behaved no differently than if we were to use a single oracle. In fact, if it weren’t for this blog post they would not have been able to deduce how they were used in conjunction with other oracles or even that they were used at all with other oracles. Just as before, all a DLC oracle does is publicly commit to and attest to outcomes of events with no requirement of knowledge about their users or even their existence.
So there you have it, arbitrary numeric outcomes executed with arbitrary payout curves and protected by a threshold of multiple oracles, all of whom are oblivious to their users’ existence.