On December 4th, 2020, Chris and I (Nadav) entered into a Discreet Log Contract (DLC) speculating on the BTC/USD price. Specifically, I took the position that over the course of a week the price would move significantly, up or down, and Chris took the position that it would not move very far.
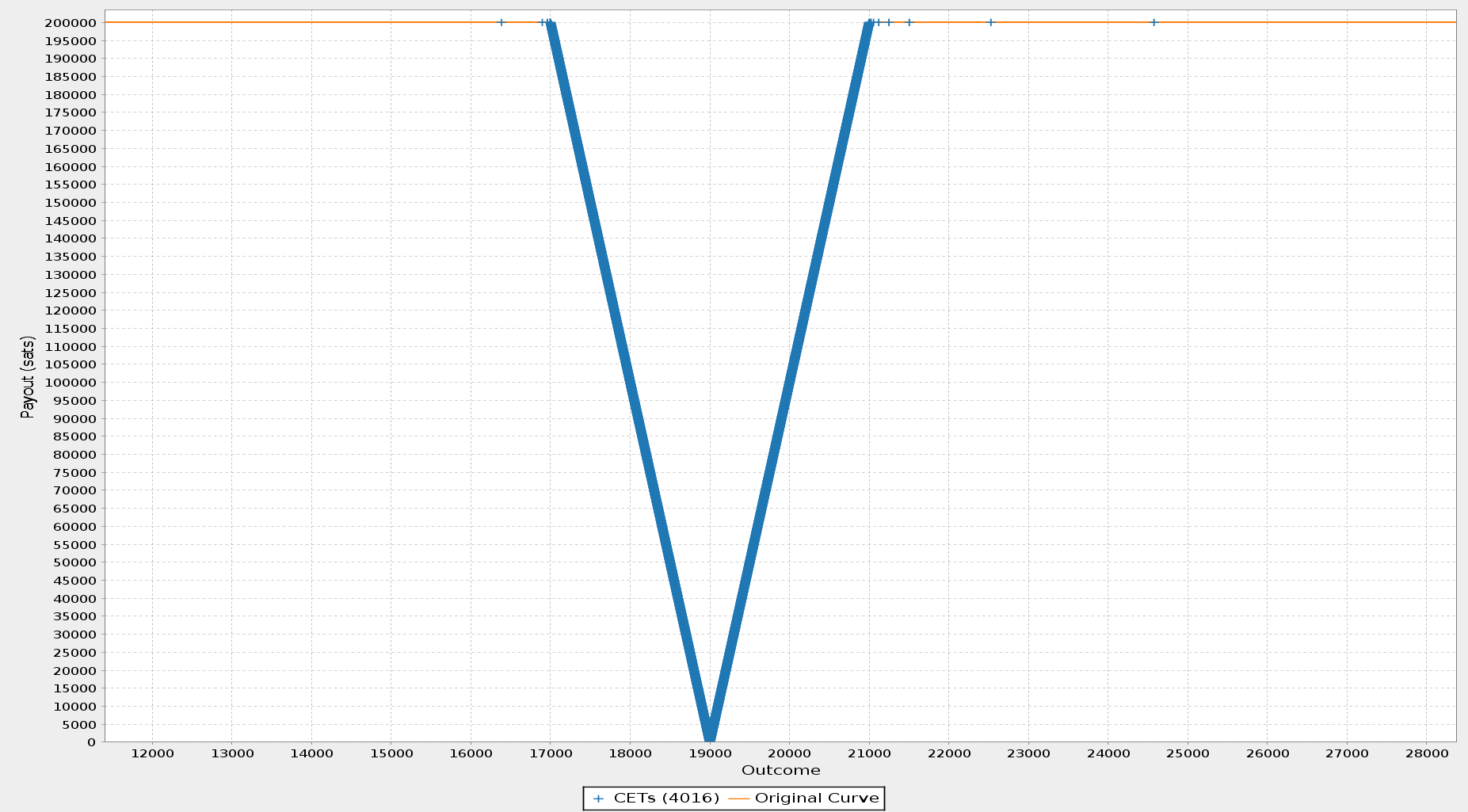
Above is my payout curve which has a flattened “V” shape where I lose all my BTC if the oracle signs the price $19,000 and win all of Chris’ BTC if the price is below $17,000 or above $21,000. These flat ends of the curve where one party gets all of the funds are called “collars”. If the oracle signs any price in-between the collars then we use this V shape to determine what our payouts are.
A DLC consists of a single on-chain funding transaction, and a set of off-chain transactions called Contract Execution Transactions (CETs). There is a single CET for every possible outcome and the outputs on the CET reflect each party’s payout for that outcome. Each CET spends the on-chain funding transaction’s 2-of-2 multisignature output and the oracle contract is enforced by making this spending contingent on an oracle signature of a specific message unique to that CET. To learn more about how DLCs work, check out our previous blog post series or the DLC work-in-progress specification which has additional resources.
In theory, this scheme supports an arbitrary number of outcomes so that Chris and I could have created a CET for every possible price that could have been signed by The Oracle of Delphi from $0 to $131,071. However, in practice this approach yields an impractical number of CETs and corresponding number of adaptor signatures which need to be generated and sent over the wire.
In the DLC whitepaper, Thaddeus Dryja mentions an optimization for numeric outcomes where rather than just signing a single number, the oracle instead signs a base and an exponent. This scheme allows collars to be compressed into a smaller number of CETs. This is because most of the time looking at the exponent alone is enough to determine that an outcome lies on a collar so that a single CET can cover a very large number of cases.
In the numeric outcome proposal of the DLC specification we extend this approach so that oracles are required to sign each bit (binary digit) of the numeric outcome separately. This enables compression of the collars even further so that only a logarithmic number of CETs is required to cover all cases on the collars, which is a negligible amount. This is the approach The Oracle of Delphi, Chris and I took to execute our DLC, with the oracle signing 17 binary digits. This allowed Chris and my contract’s collars to be condensed to fewer than 20 CETs! For a fully detailed description of the compression algorithm, see the numeric outcome proposal.
That proposal, implemented in an experimental branch of bitcoin-s, allows for the creation of contracts with arbitrary payout curves. Normally, this is accomplished by specifying some number of points on the payout curve and having the interpolating algorithm specified there “connect the dots.” Interpolating between points is also supported not only with straight lines, but also polynomial curves such as parabolas and cubics (e.g. cubic spline is supported). For my contract with Chris, this entailed specifying the end of the left collar where I win all funds at $17,000, the price at which Chris wins all funds at $19,000, and the beginning of the right collar where I win all funds at $21,000. These three points are serialized as specified and shared between me and Chris, and after that the algorithms in the specification connect lines between these points and compress the collars into just a handful of CETs. As a result, our DLC speculating about a possible space of 131,072 possible outcomes only had 4,016 CETs and was very fast to set up and execute.
The setup process involved constructing the payout curve where I simply specified the three points discussed in the previous paragraph, and from their the bitcoin-s wallet generated the funding transaction from Chris and my funding inputs, as well as the 4016 CETs and adaptor signatures of them which we sent to one another in a file. With signatures shared and verified, we broadcast the funding transaction.
At the end of the week, The Oracle of Delphi published 17 signatures of the bits 00100101011101100 which corresponds to the outcome $19,180. Sadly for me, these signatures unlocked a CET which paid me 18,000 satoshis and Chris got the other 182,000 satoshis. Specifically Chris used the adaptor signature for this CET that I had sent him last week, along with the oracle signatures to generate a valid signature from me of this CET and he then broadcast this settlement transaction. In total, the setup process took us less than a minute (not counting confirmations) and settlement took Chris mere seconds, all while leaving a very minimal on-chain footprint and keeping our contract private (that is, if we didn’t write about it).
There are two further steps that we hope to implement in bitcoin-s to improve future DLCs even more. The first is specified in the numeric outcome proposal and allows for parties to negotiate intervals over which they agree to round payouts to the nearest X satoshis. This results in staircase-looking payout curves which allows the CET compression algorithm to be run not only on the collars but also on every “step” of the staircase where some continuous interval has the same payout because not every bit of information is needed to determine which step you are on. The second future improvement is support for threshold oracle schemes, such as using 2 of 3 oracles to execute a DLC. I am currently working on a proposal for how this should be done, which will be released on the specification repository very soon!
Stay tuned for more updates and progress on Discreet Log Contract development and other cool stuff we’re working on at Suredbits!
Feel free to connect with us on Twitter @Suredbits or join our Suredbits Slack community.
If you are interested in setting up a bitcoin-s wallet, check out the bitcoin-s documentation.