The elliptic curve used by Bitcoin is called secp256k1 and it is the curve y^2 = x^3 + 7 (it is actually the finite/discrete version of this but no need to get into that here).
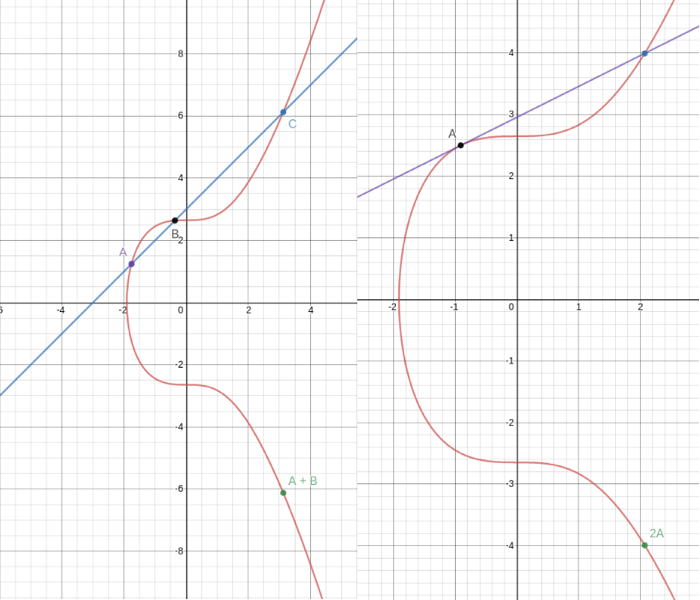
We define adding two points (A and B) together on this curve to be the process of drawing a line through them, finding the third point on the curve that intersects this line (C), and then going either straight up or straight down to take the point with the opposite y coordinate (see the left diagram). Adding a point (A) to itself uses the same process except you take the tangent line (rather than the line going through two points) as shown on the right.
It turns out that there is an efficient way to compute any multiple, x, of any point, P, that is exponentially faster than computing P + P + … + P (x copies) sequentially. And as of writing this, no one has yet to find any way of computing x from x*P (this problem is known as the Discrete Log Problem) much more efficiently than just trying every multiple of P, that is P =? x*P, 2*P =? x*P, 3*P =? x*P, … and so on. This means that if I choose some random 32 byte number, x, to be my private key, then I can quickly (much less than a second) compute x*G to be my public key (where G is called the generating point which everyone using Bitcoin agrees to use) while if someone else learns my public key, they gain no information about my private key!
What’s more, there is another nice property that adding two points together corresponds to adding their underlying scalars together: x*G + y*G = (x+y)*G and also multiplying a point by some number corresponds to multiplying the underlying scalar by that number: x*(y*G) = (x*y)*G.
Diffie-Hellman (ECDH):
(requires Bitcoin Public Keys knowledge)
Now that we have private and public keys under our belts, how do we use them for secret sharing and more generally encryption? Say that Alice and Bob have key pairs (a, A = a*G) and (b, B = b*G) respectively, and that they want to have a shared secret. Alice can compute the point a*B and Bob can likewise compute b*A … and these two points are actually the same point: (a*b)*G! Furthermore, it is impossible to recover this point if you only have knowledge of A and B. At least one of the private keys must be known in order to compute this secret point, and so this is a shared secret between Alice and Bob. This is called a Diffie-Hellman secret exchange (after its creators). Alice and Bob can now use this secret as the basis of symmetric key encryption, or any other procedure that requires a symmetric key. Note: in practice it is usually more secure to use some hash of this shared secret, since the result of a Diffie-Hellman secret exchange is not a uniformly random output.
(requires Bitcoin Public Keys knowledge)
So now we have private and public keys in our toolbox, we have everything that we need to construct (Schnorr) signatures. Say that we have a private key x and its public key P = x*G. Given a message, m, (which is really just a number) we wish to sign that message with x but without revealing anything about x. We could try to do this by using s_bad = m*x as our signature, but if we did this than anyone who knows m would be able to figure out our private key! So we do the next simplest thing, add a random number k to it: s = k + m*x … and that’s it!
This perfectly hides our private key x so long as no one knows k, which is a random secret. But how can someone else, who only knows my public key P verify this signature of m? We give them one more piece of information: R = k*G, that is, the public key for k if we treat k as a private key. Now, if we give someone R and s, all they have to do is verify that s*G = R + m*P. Why does this work? Because s*G = (k + m*x)*G = k*G + m*(x*G) = R + m*P. Essentially anyone can compute the “public key version” of our signature computation (R + m*P instead of k + m*x) and validate that this is the same as the “public key” for the signature.
One last special property of Schnorr signatures is that if you sign two different messages with the same key (x) and random secret (k) then you leak your private key since anyone can solve:
s_1 = k + m_1*x
s_2 = k + m_2*x
for k and x since there are 2 unknowns and two equations.
Contact us @Suredbits

